Oolite JavaScript Reference: Vector3D
Prototype: Object
Subtypes: none
The Vector3D class represents a geometrical vector in three-dimensional space, in cartesian representation. It is used to represent positions, headings and velocities. Explaining vector geometry is beyond the scope of this document, but there are numerous tutorials on the web.
Vector Expressions
All Oolite-provided functions which take a vector as an argument may instead be passed an array of three numbers, or an Entity (in which case the entity’s position is used). In specifications, this is represented by arguments typed vectorExpression. For example, if a and b are vectors whose values are (0, 1, 0) and (1, 0, 0) respectively, the following are equivalent:
var c = a.add(b); var d = a.add(Vector3D(1, 0, 0)); var e = a.add([1, 0, 0]); // c, d and e are now all (1, 1, 0).
Properties
x
x : Number (read/write)
The x co-ordinate of the vector.
y
y : Number (read/write)
The y co-ordinate of the vector.
z
z : Number (read/write)
The z co-ordinate of the vector.
Methods
Constructor
new Vector3D([value : vectorExpression]) : Vector3D
Create a new vector with the specified value. If no value is provided, the vector is initialized to (0, 0, 0).
add
function add(v : vectorExpression) : Vector3D
Returns the vector sum of the target and v.
See Also: subtract()
angleTo
function angleTo(v : vectorExpression) : Number
Returns the angle (in radians) between the target and vectorExpression. This is always a positive value between 0 and π.
v.angleTo(u) is equivalent to Math.acos(v.direction().dot(u.direction())).
cross
function cross(v : vectorExpression) : Vector3D
Returns the cross product of the target and vectorExpression.
See Also: dot()
direction
function direction() : Vector3D
Returns the unit vector with the same direction as the target.
v.direction() is equivalent to v.multiply(1 / v.magnitude()).
See Also: magnitude()
distanceTo
function distanceTo(v : vectorExpression) : Number
Returns the distance between the source vector and v. If v is not a vector, then if it is an Entity its position will be used; and if it is an array of three values (for example, [x, y, z] or [1, 2, 3]), it will be treated as a vector with those coordinates.
u.distanceTo(v) is equivalent to u.subtract(v).magnitude().
CAUTION: If passed an invalid v, the method will return zero, not log an error. It is also incorrect to call distanceTo on something that is not a vector. For example: this.ship.distanceTo(v) is missing position and needs to be written as this.ship.position.distanceTo(v).
See Also: squaredDistanceTo()
dot
function dot(v : vectorExpression) : Number
Returns the dot product of the target and v.
The dot product of two vectors says something how well they are aligned to each other. The dot product of two identical vectors is 1 while two vectors pointing in opposite direction result in a -1 result. Also you can't reliably compare two vectors with each other to see if they are identical. To check if vector1 == vector2 you need the dot product :
vector1.dot(vector2) > 0.999
See Also: cross()
fromCoordinateSystem
function fromCoordinateSystem(system : String) : Vector3D
Convert a vector from an abstract coordinate system to absolute coordinates. system must be a three-letter string specifying an abstract coordinate system.
Important: Vectors do not “know” which coordinate system they’re in. The script must keep track of that. If you add together vectors in different coordinate systems the result will be nonsense, just as if you added measurements in different units without appropriate conversions.
Example:
this.halfway = Vector3D(0, 0, 0.5).fromCoordinateSystem("wpu");
// Equivalent: Vector3D.interpolate([0, 0, 0], S.mainPlanet, 0.5)
See Also: toCoordinateSystem()
magnitude
function magnitude() : Number
Returns the magnitude (or length) of the vector.
See Also: squaredMagnitude(), direction()
multiply
function multiply(f : Number) : Vector3D
Returns the product of the target and f. This has the effect of scaling the vector by the factor f.
rotateBy
function rotateBy(q : quaternionExpression) : Vector3D
Apply the rotation specified by q to the target vector.
rotationTo
function rotationTo(v : vectorExpression [, maxArc : Number]) : Quaternion
Returns a quaternion corresponding to a rotation from the target vector to v. The optional parameter maxArc specifies a maximum rotation angle; if the angle between the target and v is greater than maxArc radians, a rotation of maxArc radians towards vectorExpression is generated instead.
Both the target and v must be normalized. The vectors must not be antiparallel (180° apart), since the axis of rotation is undefined in this case.
Example:
var orientation = myVector.rotationTo([0, 0, 1])
This will generate a quaternion were the forwardVector is pointing in the same direction as myVector. ([0, 0, 1] is equal to the forwardVector of the identity quaternion.)
squaredDistanceTo
function squaredDistanceTo(v: vectorExpression) : Number
Returns the square of the distance between the source vector and vector v. If v is not a vector, then if it is an Entity its position will be used; and if it is an array of three values (for example, [x, y, z] or [1, 2, 3]), it will be treated as a vector with those coordinates.
u.squaredDistanceTo(v) is equivalent to u.distanceTo(v) * u.distanceTo(v), or u.subtract(v).squaredMagnitude().
CAUTION: If passed an invalid v, the method will return zero, not log an error. It is also incorrect to call squaredDistanceTo on something that is not a vector. For example: this.ship.squaredDistanceTo(v) is missing position and needs to be written as this.ship.position.squaredDistanceTo(v).
See Also: distanceTo()
squaredMagnitude
function squaredMagnitude() : Number
Returns the square of the magnitude of the vector.
v.squaredMagnitude() is equivalent to v.magnitude() * v.magnitude().
subtract
function subtract(v : vectorExpression) : Vector3D
Returns the vector difference between the target and v.
See Also: add()
toArray
function toArray() : Array
Returns an array of the vector’s components, in the order [x, y, z]. v.toArray() is equivalent to [v.x, v.y, v.z].
toCoordinateSystem
function toCoordinateSystem(system : String) : Vector3D
Convert a vector from absolute coordinates to an abstract coordinate system. system must be a three-letter string specifying an abstract coordinate system. The target of the method must be a vector in absolute coordinates. (To convert a vector from one abstract coordinate system to another, you must first call code>fromCoordinateSystem(), then toCoordinateSystem().)
Important: Vectors do not “know” which coordinate system they’re in. The script must keep track of that. If you add together vectors in different coordinate systems the result will be nonsense, just as if you added measurements in different units without appropriate conversions.
Example:
Vector3D(0, 0, 226380).toCoordinateSystem("wpu")
// In Lave system, this returns (0, 0, 0.5).
See Also: fromCoordinateSystem()
tripleProduct
function tripleProduct(v : vectorExpression, w : vectorExpression) : Number
Returns the triple product of the target, v and w.
u.tripleProduct(v, w) is equivalent to u.dot(v.cross(w)).
Static methods
interpolate
function interpolate(u : vectorExpression, v : vectorExpression, where : Number) : Vector3D
Returns a point on the line between u and v. If where is 0, the result is u. If where is 1, the result is v. If where is 0.5, the result is half way between u and v. Values of where outside the range [0, 1] are valid; for instance, Vector3D.interpolate(u, v, -1) returns a point as far from u as v is, but in the opposite direction.
Vector3D.interpolate(u, v, where) is equivalent to u.add(v.subtract(u).multiply(where)), or u.multiply(1 - where).add(v. multiply(where)).
random
function random([maxLength : Number]) : Vector3D
Returns a vector of random length up to maxLength, in a random direction. If maxLength is not specified (or not a number), 1.0 is used. These vectors are uniformly distributed within the unit sphere, which has the effect that longer vectors are more common than shorter ones. Use Vector3D.randomDirectionAndLength() if an even length distribution is desired.
In the following image, the cloud on the left was made with the 2D equivalent of random(), and the image on the right was made with the 2D equivalent of randomDirectionAndLength().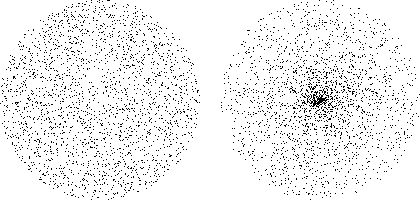
See Also: randomDirection(), randomDirectionAndLength()
randomDirection
function randomDirection([scale : Number]) : Vector3D
Returns a vector of length scale, in a random direction. If scale is not specified (or not a number), 1.0 is used.
See Also: random(), randomDirectionAndLength()
randomDirectionAndLength
function randomDirectionAndLength([maxLength : Number]) : Vector3D
Returns a vector of random length up to maxLength, in a random direction. If maxLength is not specified (or not a number), 1.0 is used. These vectors have a uniform distribution of magnitude (all lengths are equally likely), but cluster towards the origin. Use Vector3D.random() if an even spacial distribution is desired.
See Also: random(), randomDirection()